地市

新都
宜宾
雅安
乐山
绵阳
南充

新都考研辅导班

地址：新都镇兴乐北路1288号派都广场A座4楼17号

电话：028-82005799/19938477370

宜宾考研辅导班

地址：宜宾市翠屏区东街与民主路路口名城商城4楼

电话：028-82005799

雅安考研辅导班

地址：雅安市雨城区大地影院2楼

电话：028-82005799/18141378923

乐山考研辅导班

地址：乐山市中区老公园总工会5楼（老年大学旁）

电话：028-82005799/18188343237

绵阳考研辅导班

地址：绵阳市涪城区西南科技大学新区青阳中街14号

电话：028-82005799/17740904611/18111651643

南充考研辅导班

地址：南充市师大路一段210号华府丽都

电话：028-82005799/17719811995

您所在的位置：四川中公考研 > 备考资料 > 考研数学 > 2023考研数学知识点整理:欧拉方程及其解法

2023考研数学知识点整理:欧拉方程及其解法

发布日期：2022-08-18 17:42:03 来源：四川中公考研

微分方程这一章节是考研数学的常考内容，在众多考查频率较高的方程中，有一种频率相对较低，因此很容易被忽略的方程，它就是欧拉方程，下面我们一起探讨一下伯努利方程的相关问题。
要求解欧拉方程，我们首先需要识别哪些方程属于欧拉方程，它的标准形式为：，对于欧拉方程，求解思路是固定的：
首先，需要令，则有以此类推，将这些关系代回，则原方程可化为一个关于的阶常系数线性微分方程。
其次，求解此常系数线性微分方程，并将回代即可。
我们通过2021年数一考过的这道题进行详细说明。
【2021-1-5分】欧拉方程满足条件的解为
解：令，则有将上述关系式代入原微分方程，则原方程可化为化简可得解得将回代，可得由于，故
这样我们就完成了欧拉方程的求解。希望大家掌握解法，在考试中不要丢分哦。
点击查看2023考研数学知识点整理:欧拉方程及其解法完整版

考研实用工具推荐
1、考研院校专业匹配查询系统
2、近4年全国各在招院校专业复试分数线查询
3、历年调剂信息查询
4、历年各院校专业目录查询
5、历年各院校报录比查询
6、历年各院校参考书目录查询

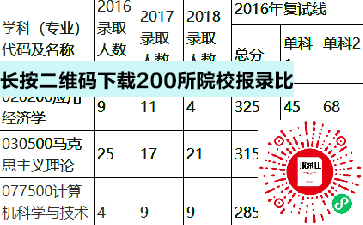
免责声明：本站所提供的内容均来源于网友提供或网络搜集，由本站编辑整理，仅供个人研究、交流学习使用，不涉及商业盈利目的。如涉及版权问题，请联系本站管理员予以更改或删除。

【责任编辑：公众号：sckaoyan365】

上一篇： 2024考研数学二阶常系数线性微分方程解的结构

下一篇： 2023考研数学浅析概率论参数估计计算思路

10秒智能择校

查看历年试题

热点推荐

备考福利站

公共课
|专业课

课程系列	班次名称	价格	免费开通
考研政治网络课堂	2026政治考研备考指导课	39	免费开通
考研政治网络课堂	考研政治五年试题精讲	199	免费开通
考研英语网络课堂	2026考研英语备考指导课	39	免费开通
考研英语网络课堂	考研英语（一、二）五年试题精讲	199	免费开通
考研数学网络课堂	2026考研数学备考指导课	39	免费开通
	考研数学五年试题精讲	199	免费开通
	考研数学常用公式整理	39	免费开通
23专业课精品课	311教育学考研入门课	11	免费开通
	333教育综合考研入门课	11	免费开通
	法律硕士（非法学）考研入门课	11	更多课程

课程系列	班次名称	价格	免费开通
经济学精品班	金融学考研入门课	咨询	免费开通
教育学精品班	经济学（初级）考研入门课	19	免费开通
教育学精品班	经济学（中级）考研入门课	19	免费开通
法学精品班	法律硕士（非法学）考研入门课	19	免费开通
法学精品班	13大热门专业课备考抢学包	19	免费开通
管理学精品班	管理学考研入门课	19	免费开通
管理学精品班	社会工作考研入门课	19	免费开通